Апробирование педагогических условий по развитию творческой активности школьников

На рис. 2.18. и 2.19. представлено процентное распределение правильных ответов учащихся ЭК и КК на контрольном и констатирующем этапах эксперимента.

Условные обозначения:

I – переведена1 фраза;

II – переведены 2 фразы;

III – переведены 3 фразы;

IV – переведены 4 фразы.

Рис. 2.18. Процентное распределение ответов у учащихся ЭК до и после формирующей программы

Представленные результаты показывают, что учащиеся ЭК на контрольном этапе смогли справиться с более трудными заданиями, требующими умения быстро переходить с одного способа рассуждения на другой уже 44% человека от всего класса, что составляет прирост на 28% учащихся. Из них справились со всеми 4 заданиями уже 4 человека (16%) экспериментального класса.

Рис. 2.19. Процентное распределение ответов у учащихся КК до и после формирующего этапа эксперимента

На контрольном этапе эксперимента в контрольном классе лишь на 4,2% возросло количество учеников которые справились со всеми легкими заданиями полностью и составляет ровно половину класса. И лишь на два ученика стало больше которые справились с 3 заданиями полностью.

На контрольном этапе в процессе изучения способности учащихся выделять существенное в ЭК и КК учащимся также не удалось выполнить все задания без ошибок. Средний показатель в ЭК составил 4,52 балла (прирост 0,48 баллов), в КК – 4,04 балла (прирост 0,12 баллов). Следовательно, и в экспериментальном и в контрольном классах способность выделять существенное возросла незначительно, но она остаётся на уровне ниже среднего (приложение 16,17).

На рис 2.20. и 2.21. отображены процентные распределения по количеству правильно выбранных существенных признаков (количество правильных ответов) у учащихся ЭК и КК на констатирующем и контрольном этапах эксперимента. При подсчете также учитывалось любое одно правильное слово, наиболее существенное для слова, стоящего перед скобками.

Условные обозначения:

I – VII – количество правильных ответов.

Рис. 2.20. Процентное распределение ответов у учащихся ЭК до и после формирующей программы

Как видно из рис. 2.20., в ЭК большая часть учащихся дали 4 правильных ответа 40% (прирост 10,8 баллов), а также по 5 ответов - 24% учеников. Правильно выделить существенные признаки по 6 и 7 ответам на контрольном этапе смогли еще по одному ученику. Больше 7 правильных ответов так ни один из учеников класса дать и не смог.

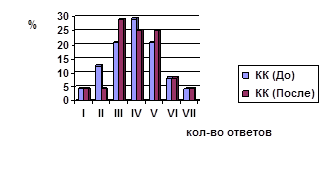
Рис. 2.21. Процентное распределение ответов у учащихся КК до и после формирующего этапа эксперимента

На контрольном этапе в КК возросло наибольшее количество трех правильных ответов на 8,3%, а по остальным вариантам правильных ответов перераспределения незначительны. В этом классе также больше 7 правильных ответов так ни один из учеников класса дать и не смог.

На третьем этапе диагностировалась способность к осуществлению творческой деятельности с помощью методики «Креативный тест Вильямса».

На контрольном этапе были получены следующие результаты:

Экспериментальная группа:

Беглость 10 баллов из 12. Учащиеся работают быстро, с большой продуктивностью. Показатель повысился по сравнению с констатирующим этапом на 1,5 балла.

Гибкость 7,8 баллов из 11. Средний уровень развития способности. Показатель повысился на 1,52 балла. Возросло количество учащихся изображающих различные категории объектов (человека, дерево, цветок, дома, животное, машина, горы, города, символические обозначения).

Оригинальность 25,44 балла из 36 (прирост на 1,48 балла).Учащихся сдерживают замкнутые контуры, чтобы сделать его частью целой картины. Они перемещаются снаружи и внутри контура. Рисунки располагаются как вне, так и внутри стимульных фигур.

Великая педагогика:

Особенности работы по обучению рассказыванию детей дошкольного возраста с ОНР
Методика работы по развитию связной речи дошкольников с ОНР освещена в ряде научных и научно-методических трудов по логопедии, таких как "Программа коррекционного обучения и воспитания детей с общим недоразвитием речи 6-го года жизни", Филичева Т. Б., Чиркина Г. В. "Подготовка к школ ...

Средства обучения математике
В дидактике термин "средства обучения" не имеет достаточно четкого определения и подчас трактуется весьма расширительно, благодаря семантике слова "средство" в русском языке. В результате к средствам обучения иногда относят даже содержание образования (И.Я. Лернер), которое &quo ...

Финансовая и хозяйственная деятельность Учреждения. Имущество и средства Учреждения
4.1 Финансовое обеспечение деятельности Учреждения осуществляется на основе нормативов финансового обеспечения деятельности, установленных в соответствии действующим законодательством. 4.2 Учреждение осуществляет приносящую доходы деятельность постольку, поскольку это служит достижению целей, ради ...